Options for the Tramo specifications
The options presented in this section are based on the TSW+ program developed by Agustin Maravall and Victor Gómez. The options available for the Tramo specification are divided into five parts. They are presented in the order in which they are displayed in the graphical interface of JDemetra+. These sections are:
To facilitate the comparison between JDemetra+ specifications and specifications used in TSW+, under each option the name of the corresponding specification and argument from the original software is given. Small variants from the original solutions are indicated by an asterisk in the tables presented in this page. For an exact description of the different parameters, the user should refer to the documentation of TSW+. Some additional explanations about the TRAMO model, its parameters and estimation procedure are given in Linearisation with the TRAMO and RegARIMA models. For the pre-defined specifications the parameters are disabled, while in the case of the user-defined specifications the user can set them individually. However, as in some cases the choice of a given value results limits the possible alternatives for other parameters, the user is not entirely free to set the parameters values. Most arguments have default values; these are given in the documentation and used in the newly created user-defined specifications unless they are changed by the user.
Estimate
The Estimate section specifies the details of the estimation procedure of the TRAMO model determined in the Regression and Arima sections.
Model span → type
–; –
Specifies the span (data interval) of the time series to be used for the estimation the Tramo model coefficients. The Tramo model is then applied to the whole series. With this argument the data early in the series can be prevented from affecting the forecasts, or, alternatively, data late in the series are excluded from the modelling span, so that they do not influence the regression estimates. The possible values of the parameter are:
- All – full time series span is considered in the modelling;
- From – date of the first time series observation is included in the pre-processing model;
- To – date of the last time series observation is included in the pre-processing model;
- Between – dates of the first and the last time series observations are included in the pre-processing model;
- Last – a specific number of observations from the end of the time series is included in the pre-processing model;
- First – a specific number of observations from the beginning of the time series is included in the pre-processing model;
- Excluding – a specific number of observations is excluded from the beginning (First) and/or end (Last) of the time series in the pre-processing model. With the options Last, First and Excluding the span can be computed dynamically on the series. The default setting is All.
Tolerance
Estimation tuning; tol
Convergence tolerance for the nonlinear estimation. The absolute changes in the log-likelihood are compared to Tolerance to check the convergence of the estimation iterations. The default setting is 0.0000001. Exact ML (Estimation tuning; incon) When this option is marked, an exact maximum likelihood estimation is performed. Alternatively, the Unconditional Least Squares method is used. However, in the current version of JDemetra+ it is not recommended to change this parameter’s value. Unit root limit (Unit roots; ubp) Limit for the autoregressive roots. If the inverse of a real root of the autoregressive polynomial of the ARIMA model is higher than this limit, the root is set equal to 1. The default parameter value is 0.96.
Transformation
The Transformation section is used to transform the series prior to estimating of the TRAMO model.
Function
Transformation; lam
Transformation of data1. The user can choose between:
- None – no transformation of data;
- Auto – the program tests for the log-level specification. This option is recommended for an automatic modelling of many series.
- Log – takes logs of data.
The default setting is Auto.
Fct
Transformation; fct
Controls the bias in the log/level pre-test (the function is active when Function is set to Auto); Fct > 1 favours levels, Fct < 1 favours logs. The default setting is 0.95.
Regression
The Regression section allows for an estimation of deterministic effects in the series with the pre-defined regression variables. These variables include user-defined variables, several types of pre-specified outliers, intervention variables and calendar effects. The pre-defined and user-defined regression variables are selected with the Variables argument.
-
Calendar $\rightarrow \ $ tradingDays $\rightarrow \ $ automatic
Trading day; itrad*This option is available when the Option parameter is set to Default.
The Trading days section of the specifcation
The Automatic option determines the manner in which the calendar effects are entered in the TRAMO model. It can be done in two ways: automatically (on the basis of the specified test) or manually. The calendar effects that are considered here are: trading days, working days and leap year effects. The significance of the Easter effect is considered in the subsequent part of this section.
- Unused – no test is performed for the calendar effects. JDemetra+ includes in the TRAMO model the calendar effects specified by the user under the Calendar $\rightarrow \ $ tradingDays $\rightarrow \ $ tradingDays and Calendar $\rightarrow \ $ tradingDays $\rightarrow \ $ LeapYear parameter options.
- FTest – the choice of the number of calendar variables to be included in the TRAMO model is based on the outcome of F-tests computed on the two models: one with the trading day variables and the other with the working day variable (F-test is performed on the coefficients of the calendar variables). The model with higher P-value is chosen, provided that it is higher than Pftd (see Calendar $\rightarrow \ $ tradingDays$\rightarrow \ $Pftd).
- WaldTest – working days are restricted to trading days. The choice of the number of calendar variables to be included in the TRAMO model is based on the outcome of the Wald test computed on that restriction. The P-value computed on the preferred model must be higher than Pftd (see Calendar $\rightarrow \ $ tradingDays $\rightarrow \ $Pftd).
The default setting is Unused.
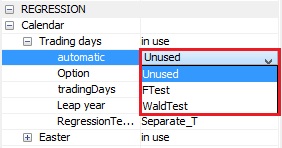
The Automatic section menu
-
Calendar $\rightarrow \ $tradingDays $\rightarrow \ $ Pftd
Trading day; pftdP-Value applied in the test specified by the automatic parameter to assess the significance of the pre-tested calendar effects and to decide if the calendar effects are included in the TRAMO model. The Pftd option is displayed when Calendar $\rightarrow \ $ tradingDays $\rightarrow \ $ automatic is set to FTest or WaldTest. The default Pftd setting is 0.01.
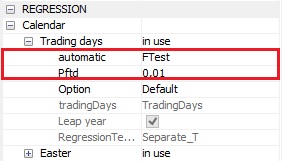
The Pftd option
-
Calendar $\rightarrow \ $tradingDays $\rightarrow \ $ option
Trading day; itrad*Specifies the type of calendar being assigned to the series. The following types of calendar estimation are available:
- None – calendar effects will not be included in the regression.
- Default – a default JDemetra+ calendar, which does not include any country-specific holidays, will be used.
- Stock – estimates day-of-week effects for inventories and other stock reported for the $w^{\text{th}}$ day of the month (to denote the last day of the month enter the number 31).
- Holidays – corresponds to the pre-defined trading day variables, modified to take into account country specific holidays. It means that after choosing this option the user should specify the type of a trading days effect under Calendar $\rightarrow \ $tradingDays $\rightarrow \ $TradingDays and a previously defined calendar that includes the country specific holidays (Calendar $\rightarrow \ $tradingDays $\rightarrow \ $holidays).
-
UserDefined – used when the user wants to specify his own trading day variables. With this option the calendar effects are captured only by the regression variables chosen by the user from the previously created list of the user-defined variables.
The default setting is Default.
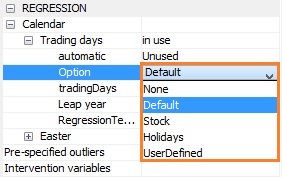
The option menu
-
Calendar $\rightarrow \ $tradingDays $\rightarrow \ $holidays
Regression variables; ireg*A list of user-defined calendars to be used to create the calendar is available when Calendar $\rightarrow \ $tradingDays $\rightarrow \ $option is set to Holidays.
The user is expected to click the Holidays field to expand a list of previously defined calendars and choose an appropriate item. The default setting is Default, which implies that the default calendar is used and no country-specific holidays are considered.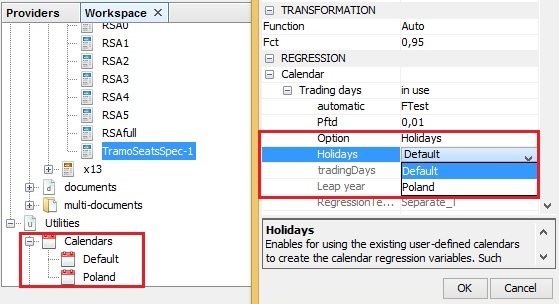
The list of calendars displayed under Holidays option corresponds to the calendars defined in the Workspace window
-
Calendar $\rightarrow \ $tradingDays $\rightarrow \ $userVariables
Regression variables; ireg, user, usertype= (...td...)*A list of the pre-defined regression variables to be included in the model. Option is available when Calendar $\rightarrow \ $ tradingDays $\rightarrow \ $option is set to UserDefined. When the user chooses the UserDefined type for a trading day effect estimation, one must specify the corresponding variables by clicking the field and choosing variables from the list. It should be noted that such variables need to be already defined, otherwise the list is empty. The default setting is Unsused.
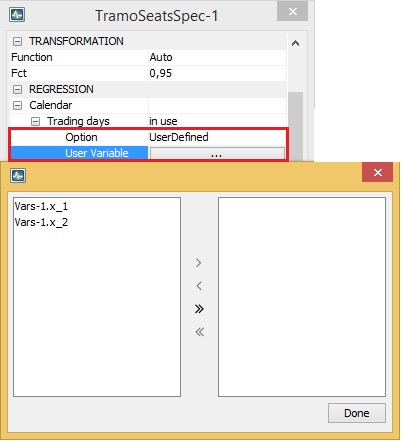
Assigning the user-defined variables to the Tramo model
-
Calendar $\rightarrow \ $tradingDays $\rightarrow \ $ tradingDays
regression variables, itradAssigns a type of a model-estimated regression effect to the pre-specified regression variables. Option is available when Calendar $\rightarrow \ $ tradingDays $\rightarrow \ $ automatic is set to Unused and Calendar $\rightarrow \ $ tradingDays $\rightarrow \ $ option is set to Default or Holidays.
Acceptable values:
- None – excludes calendar variables from the regression model.
- TradingDays – includes six day-of-the-week regression variables.
- WorkingDays – includes the working/non-working day contrast variable.
The default setting is TradingDays.
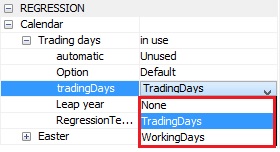
The trading days menu
-
Calendar $\rightarrow \ $tradingDays $\rightarrow \ $leapYear
regression variables; itradEnables/disables a leap-year correction. By default, the checkbox is marked, which implies that the leap-year effect correction is enabled.
-
Calendar $\rightarrow \ $ tradingDays $\rightarrow \ $ RegressionTestType
regression variables; itrad*Option for a pre-test of the trading day effects. It is not available when the Calendar $\rightarrow \ $ tradingDays $\rightarrow \ $ automatic checkbox is set to Unused. Available options:
- None – the test is not performed; the specified calendar variables are used in the model without pre-testing.
- Separate_T – a t-test is applied to each trading day variable separately. The trading day variables are included in the TRAMO model if at least one t-statistic is greater than 2.6 or if two t-statistics are greater than 2.0 (in the absolute values).
- Joint_F – a joint F-test of significance of all the trading day variables. The trading day effect is significant if the F statistic is greater than 0.95.
The default setting is Separate_T.
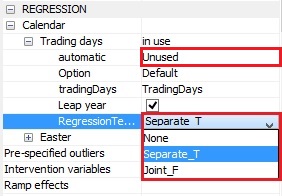
The RegressionTestType menu
-
Calendar $\rightarrow \ $ easter $\rightarrow \ $ Option
easter effect; ieast*Option for specification of presence and length of the Easter effect. Available options:
- Unused – the Easter effect is not considered;
- Standard – the Easter effect influences the period of n days strictly before Easter Sunday, where n is a Duration parameter value;
- Include Easter – the Easter effect influences the entire period (n) up to and including Easter Sunday, where n is a Duration parameter value;
- Include Easter Monday – the Easter effect influences the entire period (n) up to and including Easter Monday, where n is a Duration parameter value.
The default setting is Standard.
-
Calendar $\rightarrow \ $ easter $\mathbf{\rightarrow}$ Use Julian Easter
When marked, it enables Easter to be included, which date derives from the Julian calendar and is converted to the Gregorian calendar date. By default, the checkbox is unmarked.
-
Calendar $\rightarrow \ $ easter $\rightarrow \ $ duration
easter effect; idurDuration (length in days) of the Easter effect. The length of the Easter effect can range from 1 to 15 days. The default value is 6.
-
Calendar $\rightarrow \ $ easter $\rightarrow \ $ test
easter effect; ieastA t-test applied for the significance of the Easter effect. The Easter effect is considered as significant if the t-statistic is higher than 1.96. By default, the checkbox is marked, which implies that the t-test is used.
-
Pre-specified outliers
regression variables; –User-defined outliers are used when prior knowledge suggests that certain effects exist at known time points2. Four pre-defined outlier types, which are simple forms of intervention variables, are implemented:
- Additive Outlier (AO);
- Level shift (LS);
- Temporary change3 (TC);
- Seasonal outliers (SO).
Descriptions and formulas are available in Linearisation with the TRAMO and RegARIMA models. No pre-specified outliers are included in the pre-defined specifications. They can only be added to the user-defined specifications.
-
Intervention variables
regression variables; –The intervention variables are defined as in TSW+. Following the definition, these effects are special events known a priori (strikes, devaluations, political events, and so on). Intervention variables are modelled as any possible sequence of ones and zeros, on which some operators may be applied. Intervention variables are built as combinations of the following basic structures4:
- Dummy variables5;
- Any possible sequence of ones and zeros;
- $\frac{1}{(1 - \delta B)}$,
- $(0 < \delta \leq 1)$;
- $\frac{1}{(1 - \delta_{s}B^{s })}$,
- $(0 < \delta_{s} \leq 1)$;
- $\frac{1}{(1 - B)(1 - B^{s})}$;
where $B$ is backshift operator (i.e. $B^{k}X_{t} = X_{t - k}$) and $s$ is frequency of the time series ($s = 12\ $for a monthly time series, $s = 4\ $for a quarterly time series).
These basic structures enable the generation of not only AO, LS, TC, SO and RP outliers but also sophisticated intervention variables that are well-adjusted to the particular case. No intervention variables are included in the pre-defined specifications. They can only be added to the user-defined specifications.
-
Ramp effects
regression variables; –A ramp effect means a linear increase or decrease in the level of the series over a specified time interval $t_{0}$ to $\ t_{1}$. All dates of the ramps must occur within the time series span. Ramps can overlap other ramps, additive outliers and level shifts. The graph and formula are available in Linearisation with the TRAMO and RegARIMA models. No ramps are included in the pre-defined specifications. They can only be added to the user-defined specifications.
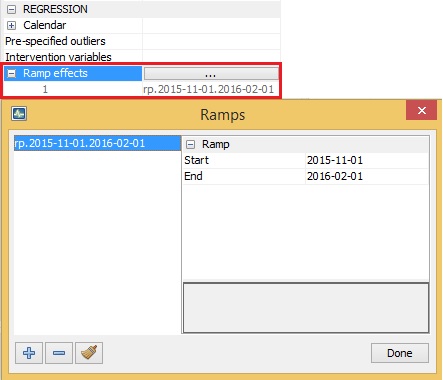
Defining the Ramp effects
-
User-defined variables
regression variables; –The user-defined variable is an external regressor included by the user in the TRAMO model. To add a user-defined variable to the model, one must specify the corresponding variable by clicking the Name field and choosing a variable from the list. It should be noted that such variables must have been previously defined (see instructions provided here) otherwise the list is empty.
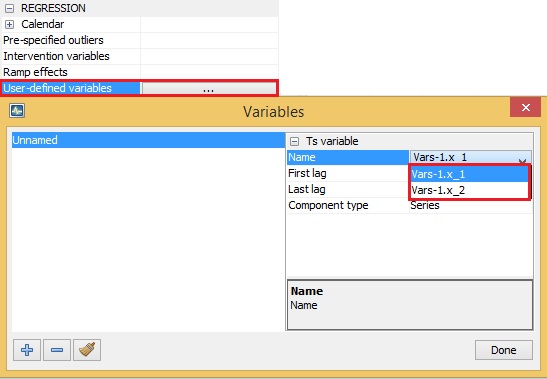
Defining the user-defined variable
The user-defined regression variable associated to a specific component should not contain effects that have to be associated with another component. Therefore, the following rules should be observed:
- The variable assigned to the trend or to the seasonally adjusted series should not contain a seasonal pattern;
- The variable assigned to the seasonal should not contain a trend (or level);
- The variable assigned to the irregular should contain neither a seasonal pattern nor a trend (or level).
The user-defined variables should cover the period of the dependent series and the appropriate number of forecasts. For the other periods, the variables are implicitly set to 0. If the forecasts are not provided, it will not alter the results of the seasonal adjustment but the forecasts of the final components will be unusable. The effect of the user-defined variable can be assigned to the:
- Trend;
- Irregular component;
- Seasonal component;
- Seasonally adjusted series;
- Undefined (a default setting), which implies that the effect is an additional component 6. With this option the regression variable is used to improve the modelling, but it is not removed from the series for the decomposition7.
The calendar component is not available in this section. Therefore, a user-defined variable assigned to the calendar effect should be added in the calendar part of the specification.
For the user-defined variable the structure of the lags can be specified using the options first lag and last lag.8 When the regression variable $x_{t}$ is introduced with first lag = $l_a$ and last lag = $l_b$, JDemetra+ includes in the TRAMO model a set of variables, $x_{t - l_{a}}$,…,$\ x_{t - l_{ b}}$,and estimates the respective regression coefficients called the impulse response weights. To include only the first lag $(x_{t - 1})\ $of the user-defined variable $(x_{t})\ $in the Tramo model, the user should put first lag = last lag = 1. If for a monthly series one puts first lag = 0 and last lag = 11, it means that in addition to the instantaneous effect of the user-defined variable, also the effects of 11 lagged explanatory variables are included in the model. In this case the set of estimated coefficients, called a transfer function, describe how the changes in $x_{t}$ that took place over a year are transferred to the dependent variable.
However, the lagged variables are often collinear, so that caution is needed in attributing much meaning to each coefficient.9 No user-defined variables are included in the pre-defined specifications. They can only be added to the user-defined specifications. -
Fixed regression coefficients
regression variables; –For the pre-specified regression variables this option specifies the parameter estimates that will be held fixed at the values provided by the user. To fix a coefficient the user should undertake the following actions:
- Choose the transformation (log or none).
- Define some regression variables in the Regressors specification.
- Push on the fixed regression coefficients editor button in the User-defined variables row.
- Select the regression variable from the list for which the coefficient will be fixed.
- Save the new setting with the Done button.
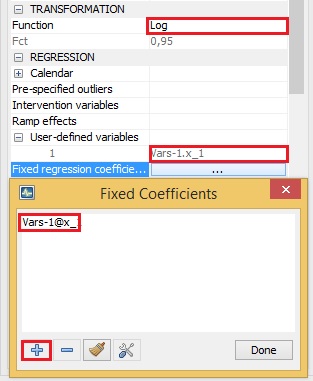
Fixing the coefficient of the user-defined variable
Outliers
The Outliers section enables the user to perform an automatic detection of additive outliers, temporary change outliers, level shifts, seasonal outliers, or any combination of these four basic outlier types, using the specified model.
TRAMO specification – options for the Outliers section
-
Is enabled
outliers; iatipEnables/disables the automatic detection of outliers in the span determined by the Detection span option. By default, the checkbox is marked, which implies that the automatic identification of outliers is enabled.
-
Use default critical value
outliers; vaThe critical value is automatically determined by the number of observations in the interval specified by the Detection span option. When Use default critical value is disabled, the procedure uses the critical value inputted in the Critical value item (see below). Otherwise, the default value is used (the first case corresponds to "critical = xxx"; the second corresponds to a specification without the critical argument). It should be noted that it is not possible to define a separate critical value for each outlier type. By default, the checkbox is marked, which implies that the automatic determination of the critical value is enabled.
-
Critical value
outliers; vaThe critical value used in the outlier detection procedure. The option is active once Use default critical value is disabled. By default, it is set to 3.5.
-
Detection span $\rightarrow \ $ type
outliers; int1, int2*A span of the time series to be searched for outliers. The possible values of the parameter are:
- All – full time series span is considered in the modelling;
- From – date of the first time series observation included in the pre-processing model;
- To – date of the last time series observation included in the pre-processing model;
- Between – date of the first and the last time series observations included in the pre-processing model;
- Last – number of observations from the end of the time series included in the pre-processing model;
- First – number of observations from the beginning of the time series included in the pre-processing model;
- Excluding – number of observations excluded from the beginning (specified in the first field) and/or end of the time series (specified in the last field) of the pre-processing model.
With the options Last, First, Excluding the span can be computed dynamically on the series. The default setting is All.
-
Additive
outliers; aio*Automatic identification of additive outliers. By default, this option is enabled.
-
Level shift
outliers; aio*Automatic identification of level shifts. By default, this option is enabled.
-
Transitory change
outliers; aio*Automatic identification of transitory changes. By default, this option is enabled.
-
Seasonal outlier
outliers; aio*Automatic identification of seasonal outliers. By default, this option is disabled.
-
EML estimation
outliers; imvxThe estimation method used in the automatic model identification procedure. By default, the fast method of Hannan-Rissanen is used for parameter estimation in the intermediate steps of the automatic detection and correction of outliers. When the checkbox is marked the exact maximum likelihood estimation method is used.
-
TC rate
outliers; deltatcThe rate of decay for the transitory change outlier. It takes values between 0 and 1. The default value is 0.7.
Arima
Identification of the ARIMA part of the Tramo model can be done either in an automatic way or by the user, who specifies the appropriate parameters. This choice is controlled by the Automatic option and results in a list of parameters specific to the chosen ARIMA identification procedure. When the Automatic option is marked, the order of the ARIMA model results from the automatic identification procedure. The maximum order of the regular polynomials is 3, and the maximum order of seasonal polynomials is 1. The parameters available for automatic model identification are presented below.
TRAMO specification – options for the automatic identification of the ARIMA model
-
Automatic
automdl; ami; idif, inic*When marked it enables an automatic modelling of the ARIMA model.
-
Accept Default
Controls whether the default model (ARIMA(0,1,1)(0,1,1)) may be chosen in the first step of the automatic model identification. More explicitly, if the Ljung-Box Q-statistics for the residuals is acceptable, the default model is accepted and no further attempt will be made to identify another one. By default, the Accept Default option is false.
-
Cancelation limit
ami; cancelA limit for the AR and the MA roots to be assumed equal. This option is used in the automatic identification of the differencing order. If the difference in moduli of an AR and an MA root (when estimating ARIMA(1,0,1)(1,0,1) models in the second step of the automatic identification of the differencing polynomial) is smaller than Cancelation limit, the two roots cancel out. The default parameter value is 0.05.
-
Initial UR (Diff.)
ami; ub1The threshold value for the initial unit root10 test in the automatic differencing procedure. When one of the roots in the estimation of the ARIMA(2,0,0)(1,0,0) plus mean model, which is performed in the first step of the automatic model identification procedure, is larger than First unit root limit, in modulus, it is set equal to unity. This value should be less than 1 and greater than 0.8. The default parameter value is 0.97.
-
Final UR (Diff.)
ami; ub2A unit root test in the automatic differencing procedure. When one of the roots in the estimation of the ARIMA(1,0,1)(1,0,1) plus mean model, which is performed in the second step of the automatic model identification procedure, is larger than Second unit root limit, in modulus, it is checked if there is a common factor in the corresponding AR and MA polynomials of the ARMA model that can be cancelled (see Cancelation limit)). If there is no cancellation, the AR root it is set equal to unity (i.e. the differencing order changes). The value of the Second unit root limit should be less than 1 and greater than 0.8.The default parameter value is 0.91.
-
Arma limit
ami; tsigThe threshold value for t-statistics of ARMA coefficients used for the final test of a model parsimony11. If the highest order of ARMA coefficient has a t-value less than this value in magnitude, JDemetra+ will reduce the order of the model. The value given for ArmaLimit is also used for the final check of the constant term; if the constant term has a t-value less than ArmaLimit in magnitude, the program will remove the constant term from the set of regressors. The ArmaLimit value should be greater than zero. The default parameter value is 1.
-
Reduce CV
automdl; reducecvThe percentage by which the outlier critical value will be reduced when the preferred model is found to have a Ljung-Box Q-statistic with an unacceptable confidence coefficient. The parameter should be between 0 and 1, and will only be active when automatic outlier identification is selected. The reduced critical value will be set to (1−ReduceCV)×CV, where CV is the original critical value. The default parameter value is 0.12.
-
LjungBox limit
Acceptance criterion for the confidence intervals of the Ljung-Box Q-statistic. If the Ljung-Box Q-statistics for the residuals of a final model (checked at lag 24 if the series is monthly, 16 if the series is quarterly) is greater than LjungBox limit, the model is rejected, the outlier critical value is reduced, and model and outlier identification (if specified) is redone with a reduced value (see the Reduce CV argument). After two unfruitful attempts, a default model (usually ARIMA(3,1,1)(0,1,1)) will be used. The default parameter value is 0.95.
-
Compare to default
ami; amicompIf marked, it compares the model identified by the automatic procedure to the default model (ARIMA(0,1,1)(0,1,1)) and the model with the best fit is selected. The criteria for a comparison are the residual diagnostics from the automatically identified model and those of the default model (the residual standard error and the confidence coefficient of the Ljung-Box Q-statistic), the number of outliers and the structure and estimated parameters of the model identified by the automatic procedure. The comparison is done because the default model is robust and departure from this model can be unstable. By default, the Compare to default option is false.
When the Automatic checkbox in the Arima section is unmarked, JDemetra+ allows the user to specify the structure of the ARIMA part of the Tramo model. Initial values for the individual AR and MA parameters can be specified for the iterative estimation. Also, individual parameters can be held fixed at these initial values while the rest of the parameters are estimated. The options available here correspond to the original X-13ARIMA-SEATS arima spec with some limitations. JDemetra+ does not allow for operators with missing lags. Also the maximum lag is reduced in comparison with Win X-13.
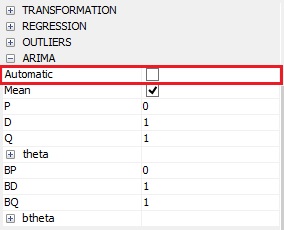
A checkbox for switching bewteen manual and automatic choice of the Arima model
Individual parameters can be held fixed at these initial values while the rest of the parameters are estimated. However, users should not specify initial values for the MA parameters that yield the MA polynomial with roots inside the unit circle.
TRAMO specification – options for manual identification of the ARIMA model
-
Automatic
ami; idif, inicWhen unmarked it enables the user to enter the parameters of the ARIMA model.
-
Mean
mean; imeanWhen marked it is considered that the mean is part of the ARIMA model (it depends greatly on the chosen model).
-
P
arima; pThe order of the non-seasonal autoregressive polynomial. The maximum order of the non-seasonal autoregressive polynomial is 4. The default value is 0.
-
phi
arima; phi, jprCoefficients of the non-seasonal, autoregressive polynomial (AR). If this is used, a label should be assigned to each non-seasonal AR parameter in the model to indicate the way in which it was estimated. The choice can be made from:
- Undefined – estimates a parameter without the use of any user-defined input (the default value).
- Initial – estimates a parameter using as initial condition the value defined by the user.
- Fixed – holds a parameter fixed during estimation at the value defined by the user.
-
D
arima; dNon-seasonal differencing order. The maximum number of non-seasonal differences is 2. The default value is 1.
-
Q
arima; qThe order of the non-seasonal moving average polynomial. The maximum order of the non-seasonal moving average polynomial is 4. The default value is 1.
-
theta
arima; th, jqrCoefficients of the parameters of the non-seasonal, moving average polynomial (MA). If this is used, a label should be assigned to each non-seasonal MA parameter in the model to indicate the way in which it was estimated. The choice can be made from:
- Undefined – estimates a parameter without the use of any user-defined input (the default value).
- Initial – estimates a parameter using as initial condition the value defined by the user.
- Fixed – holds a parameter fixed during estimation at the value defined by the user.
-
BP
arima; bpThe order of the seasonal autoregressive polynomial. The default value is 0.
-
Bphi
arima; bphi, jpsCoefficients of the seasonal autoregressive polynomial (AR). If this is used, a label should be assigned to each seasonal AR parameter in the model to indicate the way in which it was estimated. The choice can be made from:
- Undefined – estimates a parameter without the use of any user-defined input (the default value).
- Initial – estimates a parameter using as initial condition the value defined by the user.
- Fixed – holds a parameter fixed during estimation at the value defined by the user.
-
BD
arima; bdSeasonal differencing order. The maximum number of seasonal differences is 1. The default value is 1.
-
BQ
arima; bqThe order of the seasonal moving average polynomial. The maximum order of the seasonal moving average polynomial is 1. The default value is 1.
-
Btheta
arima; bth, jqsCoefficients of the parameters of the seasonal moving average polynomial (MA). If this is used, each seasonal MA parameter in the model requires a label that indicates the way in which it was estimated. The choice can be made from:
- Undefined – estimates a parameter without the use of any user-defined input. (the default value).
- Initial – estimates a parameter using as initial condition the value defined by the user.
- Fixed – holds a parameter fixed during estimation at the value defined by the user.
-
The test for log-level specification used by TRAMO is based on the maximum likelihood estimation of the parameter $\lambda$ in the Box-Cox transformations (which is a power transformation such that the transformed values of the time series $\text{y }$are a monotonic function of the observations, i.e.
The program first fits two Airline models (i.e. ARIMA (0,1,1)(0,1,1)) to the time series: one in logs ($\lambda = 0$), other without logs ($\lambda = 1$). The test compares the sum of squares of the model without logs with the sum of squares multiplied by the square of the geometric mean in the case of the model in logs. Logs are taken in the case this last function is the maximum, GÓMEZ, V., and MARAVALL, A. (2009). ↩
-
Definitions from ‘X-12-ARIMA Reference Manual’ (2011). ↩
-
In the TRAMO/SEATS method this type of outlier is called transitory change. ↩
-
See GÓMEZ, V., and MARAVALL, A. (1997). ↩
-
Dummy variable is the variable that takes the values 0 or 1 to indicate the absence or presence of some effect. ↩
-
The convention for assigning the effects of the user-defined regressors to the components is based on the TRAMO/SEATS solution. The original X-12-ARIMA program does not provide the same functionality. The effect of additional component (option Undefined) is a special feature introduced in the original X-12-ARIMA program and not available in TRAMO/SEATS. ↩
-
A typical example could be a variable that measures the weather conditions: introducing them could improve the linearization; however, these effects are not allocated to a specific component. On the contrary, the impact of this variable will be split between all components. ↩
-
More details and examples can be found in MARAVALL, A. (2008). ↩
-
MAKRIDAKIS, S., WHEELWRIGHT, S.C., and HYNDMAN, R.J. (1998). ↩
-
A time series $x_{t}$ is said to have a unit root if it can be modelled as $x_{t} = \phi_{0} + \phi_{1}y_{t - 1}$ and $\phi_{1} = 1.$ ↩
-
Parsimonious models are those which have a great deal of explanatory power using a relatively small number of parameters. Balanced models are models for which the order of the combined AR and differencing operators is equal to the order of the combined MA operator (see GÓMEZ, V., and MARAVALL, A. (1997)). ↩